| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 이진탐색
- Binary Search Proof
- 선택정렬 증명
- Proof Selection Sort
- BERT
- ChatGPT 설명
- chatGPT
- 이진탐색 증명
- GPT-3
- Discrete Wavelet Transform
- Selection Sort
- binary search
- 선택정렬
- haar matrix
- Today
- Total
Just Do IT
이미지 압축 (Image Compression) - Haar Matrix 구현 (2) (numpy, PIL, pylab) 본문
이미지 압축 (Image Compression) - Haar Matrix 구현 (2) (numpy, PIL, pylab)
풀용 2022. 2. 2. 22:41파일 준비
해당 과제는 C언어로 수행했었고 이미지를 행렬화 하기 위한 함수가 24비트 비트맵 이미지와 호환되었기 때문에 24비트 비트맵 파일로 프로젝트를 진행했다. 이미지는 이미지 처리에 항상 등장하는 레나 이미지로 했다.

1. Image Load
import numpy as np
from PIL import Image
import matplotlib.pylab as plt배열 연산에 사용할 numpy, 이미지 로드와 array 변환, 이미지 저장에 이용할 Pillow, 배열의 시각화를 위한 matplotlib의 pylab을 import 해주었다.
img_lena = Image.open('./lena_gray.bmp')
img_lena.size
imgWidth = img_lena.size[1]
imgHeight = img_lena.size[0]
print(imgWidth,imgHeight)output:
512 512size함수의 인덱싱을 통해 width와 height를 구했다.
2. 이미지를 array로 변환하기.
image_lena_arr = np.array(img_lena)
plt.imshow(image_lena_arr)
plt.axis('off')
plt.show()output:

numpy의 array로 변환 후 matplotlib으로 사진이 잘 나타나는 것을 알 수 있다.
image_lena_arr.sizeoutput:
786432512 * 512 * 3 = 786,432로 512 * 512 개의 픽셀당 3개의 RGB값 모두 표현되어 있다.
3. RGB 값중 하나의 값만 가져오기
image_lena_arroutput(일부):
array([[[162, 162, 162],
[162, 162, 162],
[162, 162, 162],
...,
[170, 170, 170],
[155, 155, 155],
[128, 128, 128]],
[[162, 162, 162],
[162, 162, 162],
[162, 162, 162],
...,output을 보면 gray scale image를 사용했기 때문에 RGB값이 모두 같은 것을 알 수 있다. 따라서 계산을 빠르고 간편하게 하기 위해 RGB 값중 하나의 값만 불러 array로 저장하는 작업이 필요하다.
Alst = [] # RGB중 하나의 값만 담을 Matrix
for i in range(imgHeight):
arr = []
for j in range(imgWidth):
arr.append(image_lena_arr[i,j,0])
Alst.append(arr)위의 output을 보면 하나의 픽셀이 3개의 element가 들어있는 리스트로 표현됐고 한 줄의 픽셀이 하나의 리스트에 들어있는 것을 알 수 있다.
쉽게 표현하자면
[[[픽셀],[픽셀], . . .], -> 첫번째 줄
[[픽셀],[픽셀], .....], -> 두번째 줄
...]
픽셀 = R,G,B 값
이런식의 총 3차원 배열로 이루어져 있다.
따라서 한 픽셀당 첫번째 값을 Alst에 append하는 과정을 진행한다. 리스트가 바뀌는 부분은 다음줄로 넘어가는 부분이다.
A = np.array(Alst)이후 계산을 위해 array로 변환한다.
4. Haar Matrix 만들기
이제 이 프로젝트의 핵심이 되는 부분이다. Haar Matrix를 만드는 방법은 stackoverflow에서 찾았다. 파이썬으로된 답변밖에 없어서 C언어로 내부 함수까지 구현하는데 정말정말정말정말 애먹었었다.. 이번에 느꼈다 파이썬으로 하면 얼마나 쉽고 간편하게 끝낼 수 있는지.. 넘파이 짱...
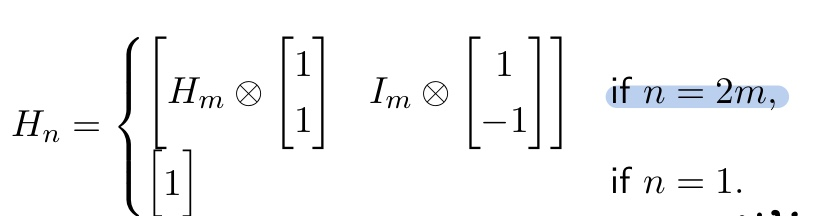
def makeHaarMatrix(n):
if n > 2:
h = makeHaarMatrix(n / 2)
else:
return np.array([[1, 1], [1, -1]])
# calculate upper haar part
h_n = np.kron(h, [1, 1])
# calculate lower haar part
h_i = np.kron(np.eye(len(h)), [1, -1])
# combine parts
h = np.vstack((h_n, h_i))
return hHaar Matrix는 재귀구조를 이용하여 만들 수 있다. n이 2가 될 때 까지 계속 재귀를 돈다. 그 이후 H의 kronecker product와 I의 kronecker product를 따로 진행 한 후 두 matrix를 합치는 방식이다. I는 Identity matrix이다.
그리고 여기서 만들어진 행렬은 다음 재귀 함수로 넘어가고 넘어가고 해서 최종 Haar Matrix가 만들어진다.
Haar = makeHaarMatrix(imgWidth)
Haar = Haar.TimgWidth 크기의 Haar matrix를 만든다. 그냥 써도 되지만 교수님의 교재와 같게 만들어 주기 위해서 transpose를 진행했다.
def normalize(h):
norms = np.linalg.norm(h, axis=0)
return h/norms
normH = normalize(Haar)
normHT = normH.T이후 normalize를 진행한다. orthonomal matrix를 만들어서 H * H^T의 값이 Identity matrix가 될 수 있게 하기 위해서이다.
5. Compression 진행하기
# B = H' * A * H
B1 = np.matmul(normHT,A)
B = np.matmul(B1,normH)Haar Matrix를 이용해서 low frequency와 high frequency를 구분짓는다. low frequency data는 좌측 상단으로, high frequency data는 우측 하단으로 몰린다.
def cut(h, n):
zeroMat = np.zeros_like(h)
zeroMat[:n,:n] = h[:n,:n]
return zeroMat
n = 128
Bhat = cut(B, n)high frequency data를 절삭하는 과정이다. n에 따라서 사진의 화질이 결정된다. 당연히 n 을 높일 수록 데이터가 덜 절삭되고 화질이 원본과 가까워 진다. 하지만 그만큼 행렬이 커지면서 저장 용량도 커지게 된다.
6. Compression 해체 하기
# Ahat = H * Bhat * H`
Ahat1 = np.matmul(normH,Bhat)
Ahat = np.matmul(Ahat1,normHT)절삭된 행렬을 복구 시키는 과정이다. 위에서 normalize를 했기 때문에 H와 H^T를 반대로 곱해주면 Identity가 되고 이미지를 복구 시킬 수 있다.
7. 이미지로 변환하기
# 원래의 Matrix(R,G,B)로 복원
Are = []
for i in range(imgHeight):
lst = []
for j in range(imgWidth):
lst2 = []
for z in range(3):
lst2.append(Ahat[i,j])
lst.append(lst2)
Are.append(lst)앞에서 계산을 효율적으로 진행하기 위해 R,G,B의 값 중 하나만 가져와서 사용했다. 다시 이미지로 만들기 위해선 RGB 값으로 만들어야 한다.
Are = np.array(Are, dtype = 'u1')이후에 list를 array로 변환해야 하는데 data type를 unsigned int8로 바꾸어 줘야한다. dtype를 따로 주지 않고 이미지 변환을 했을 때 오류가 발생했다. 따라서 원래 이미지의 데이터 타입인 unit8로 변환해야한다.
plt.imshow(Are)
plt.axis('off')
plt.show()output:

n을 128로 했을 때 이미지이다. 이미지 화질이 그렇게 잘 보이지 않는 것 같아서 n을 64로 줄여봤다.
n = 64 output:

이미지의 화질이 크게 차이나는 것을 볼 수 있다.
resultImg = Image.fromarray(Are)
resultImg.save('result%d.bmp'%n)이후 array를 이미지로 바꿔주고 저장하면 끝난다.
이 교수님의 과제는 찾아도 안나오고 정말 어렵고 시간도 많이 투자해야 하지만 얻어가는 것이 정말 많다. 수업 또한 노력하면 노력할수록 얻어가는 것이 많은 수업이였다.
'데이터사이언스-기초수학 > 선형대수학' 카테고리의 다른 글
| 이미지 압축 (Image Compression) - Haar Matrix 구현 (3) 심화 (1) | 2022.02.03 |
|---|---|
| 이미지 압축 (Image Compression) - Haar Matrix 구현 (1) (0) | 2022.02.02 |


