| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Binary Search Proof
- 이진탐색
- haar matrix
- 선택정렬 증명
- 선택정렬
- Discrete Wavelet Transform
- 이진탐색 증명
- BERT
- ChatGPT 설명
- GPT-3
- chatGPT
- Selection Sort
- binary search
- Proof Selection Sort
- Today
- Total
Just Do IT
배열(Array) - Pack, UnPack, Sort, UnSort 본문
Array란?
동일한 Type을 가진 element가 연속된 주소에 저장되는 자료구조를 말한다.
장점: n개의 데이터중 k번째 데이터 access가 상수시간에 가능하다. 즉, Search가 빠르다.
단점: 크기 변화 비용이 크기 때문에 Insert, Delete가 느릴 수 있다.
변화가 없거나 드문 자료의 경우 사용이 적합하다.
Pack
Pack은 element를 왼쪽으로 밀어 놓는 것을 말한다.
Pack
| Index | 1 | 2 | 3 | 4 |
| Data | 1 | 5 | 2 | X |
UnPack
| Index | 1 | 2 | 3 | 4 |
| Data | 1 | X | 5 | 2 |
Packed, UnSorted
가장 간단한 방법이다. 앞에서 부터 Insert하면 되고 Delete를 할 때는 배열의 마지막 element값을 Delete되는 Index에 넣으면 된다.

C++로 자료구조를 배웠기 때문에 C++처럼 코드를 구현했다. 사실 Python으로는 훨씬 간단하게 할 수 있다.
성능
Search: O(n)
Insert: [Search,O(n)] -> O(1) (Search를 한 후 Insert)
Delete:[Search,O(n)] -> O(1) (Search를 한 후 Delete)
Packed, Sorted
Sort를 하면 Binary Search를 사용할 수 있기 때문에 Search시간이 짧아진다.
대신 Insert와 Delete에 배열을 밀거나 당겨야 한다.
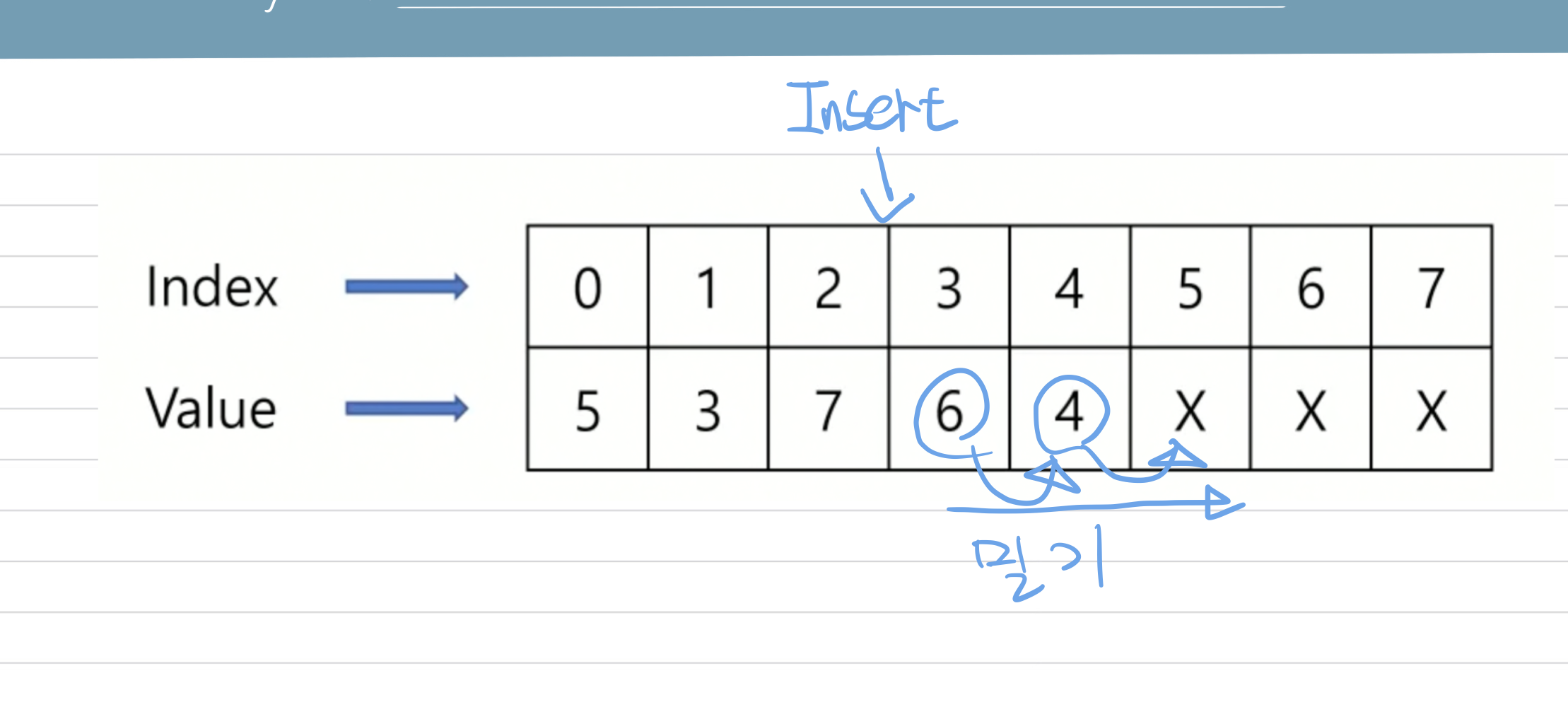
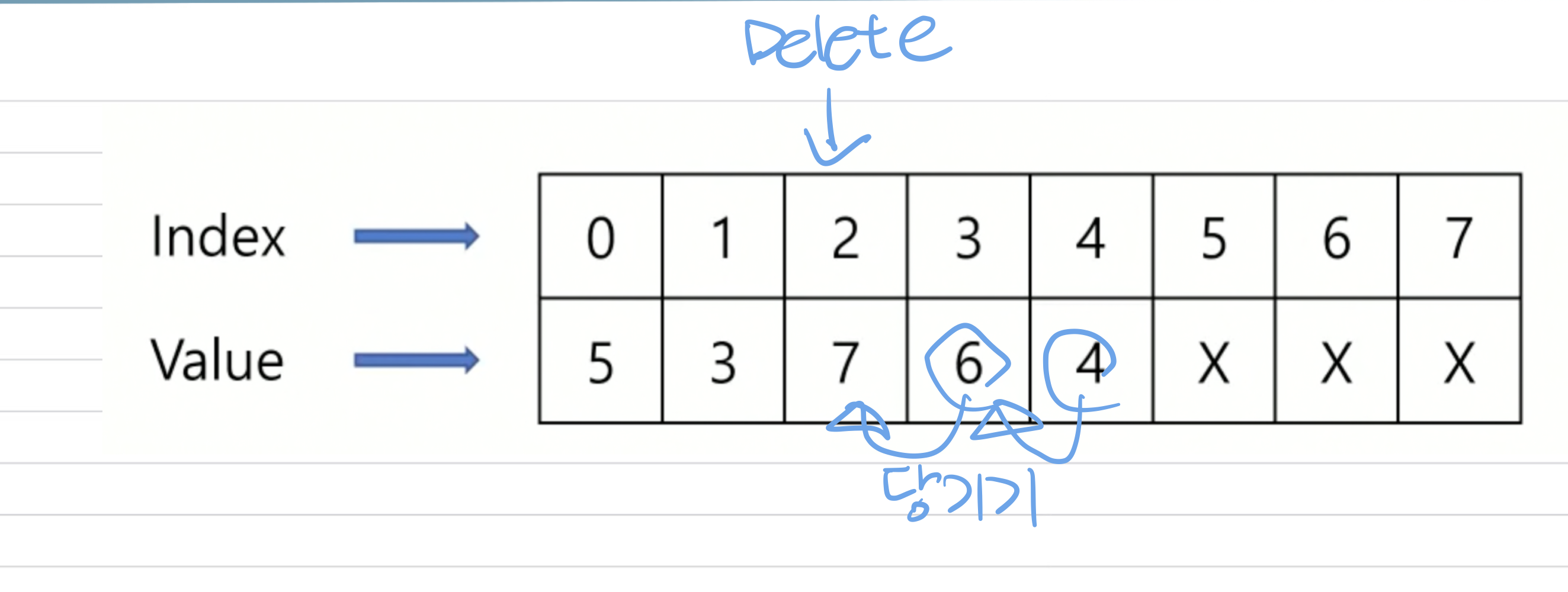
성능
Search: O(log n)
Insert: [Search, O(log n)] -> O(n)
Delete: [Search, O(log n)] -> O(n)
UnPacked, Sorted
굉장히 이상해 보일 수 있지만 충분히 가능하다. Search가 O(n)시간 걸리지만 Delete할 때 Value를 건들이지 않음으로써 O(log n)시간에 가능하다.
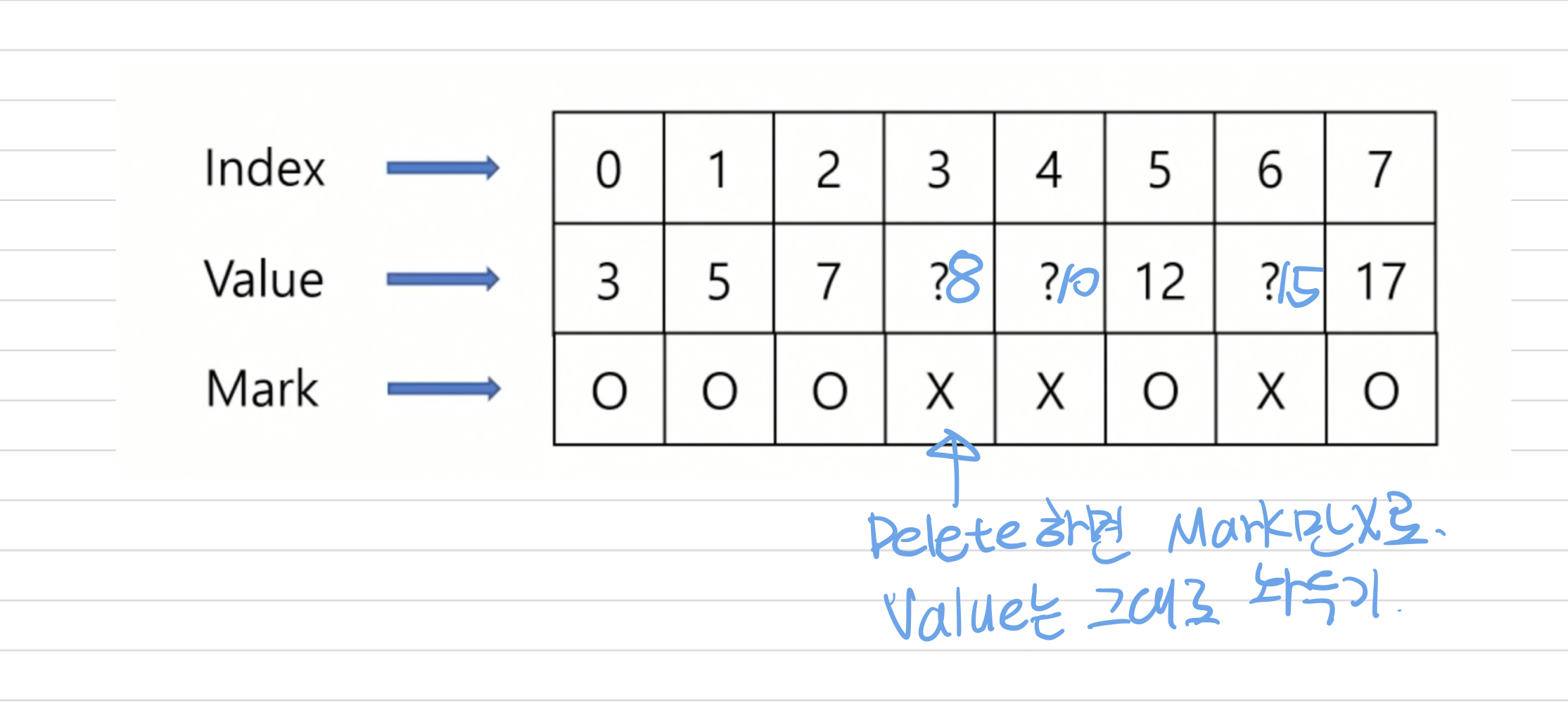
- 가장 처음 Insert할때는 Pack처럼 차례대로 Insert 한다.
- Delete를 하면 단순히 Mark만 X로 변경한다.
- 위 그림처럼 Value는 그대로 있기 때문에 Binary Search가 가능하다. 따라서 Search를 O(log n)에 수행 할 수 있다.
- 대신 Insert때 Mark가 X로 되어있는지 찾아야하기 때문에 코드가 복잡해진다.
성능
Search: O(log n)
Insert: [Search, O(log n)] -> O(n)
Delete: [Search, O(log n)] -> O(1)
'자료구조-알고리즘(Python) > 자료구조' 카테고리의 다른 글
| 동치관계(Equivalence Relation) - DFS(Stack) & LinkedList,List (0) | 2022.06.30 |
|---|---|
| 동치관계(Equivalence Relation) - DFS(Stack) & Matrix (0) | 2022.06.30 |
| 미로찾기 - BFS(Queue) (0) | 2022.06.28 |
| 미로찾기 - DFS(Stack) (0) | 2022.06.28 |
| 수학적 귀납법에서 참을 가정하는 이유 (0) | 2022.06.28 |



