| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- haar matrix
- chatGPT
- Proof Selection Sort
- 이진탐색
- Binary Search Proof
- GPT-3
- BERT
- Selection Sort
- 선택정렬 증명
- 이진탐색 증명
- Discrete Wavelet Transform
- binary search
- 선택정렬
- ChatGPT 설명
- Today
- Total
Just Do IT
[논문리뷰] Generative Adversarial Networks 생성적 적대 신경망(GAN) - 1 본문
들어가며
AI학문의 대부 Yoshua Bengio의 제자인 Ian Goodfellow가 만들어낸 정말 기발한 아이디어가 녹아있는 논문이다. 처음 GAN의 아이디어를 들었을 때 '어떻게 이런 생각을 할 수 있었을까'라는 생각이 들 정도로 충격을 받았던 기억이 있다. GAN은 논문이 처음나온 2014년부터 지금까지 꾸준히 연구되고 성장하는 분야로 noise로 시작해서 새로운 이미지를 '생성' 해내는 창의적인 모델이다. 먼저 이 글에서는 GAN의 기본 개념을 rough하게 다뤄보려고 한다. VAE와의 차이, KL divergence와 JS divergence 등등 수학적인 이론은 따로 다룰 예정이다.
0. Abstract

이 논문에서는 동시에 두가지 모델을 train하는 방법론을 제시한다. 그 모델은 data distribution을 capture하는(real image를 흉내내는) generative model G와 G에서 온 data가 아닌 real image에서 온 데이터의 확률을 측정하는 discriminative model D이다. G는 D가 실수할 확률(G에서 온 data를 real image에서 온 data로 착각할 확률)을 극대화 하도록 한다. 임의의 함수 G와 D에 대해서 unique solution이 있다면(optimal한 점이 있다면) G는 real image를 복원하고 D는 어디서나 1/2의 정답 확률을 갖는다.
- D가 1/2의 정답 확률을 갖는 이유는 G가 training data 즉, real image를 정확하게 복원하게 된다면 D는 자신에게 들어온 data가 어디서 왔는지 맞출 수 없기 때문이다. 따라서 random하게 맞거나 틀리기 때문에 1/2의 확률을 갖는다
논문에서 G와 D는 backpropagation으로 훈련 될 수 있고 Markov chains나 unrolled approximate inference networks가 필요하지 않는다고 주장한다.
- GAN이전의 generative model의 흐름이 markov chains나 unrolled approximate inference networks가 필요했던 모양이다. generative model의 역사는 앞으로 더 공부할 부분인 것 같다.
- https://stats.stackexchange.com/questions/361871/in-ian-goodfellow-et-als-paper-generative-adversarial-networks-why-do-they-s 나랑 비슷한 궁금증을 품었던 사람이 있었고 그에 대한 의견들이 달려있다
1. Introduction

논문에서는 딥러닝은 다양한 분야 특히 image, language등의 input을 특정 class label에 매핑 시키는 task에서 성공을 거뒀다고 주장한다. 하지만 generative model은 MLE와 그에 연관된 상호작용하는 확률 연산들을 approximating하는게 어렵고 linear unit들의 이점을 generative context에서 살리는것이 어렵기 때문에 성공적이지 못했다고 주장한다.
- 이 문단에서 generative model이 성공적이지 못했던 이유가 와닿지 않는다. 이 역시 이전의 generative model에 대한 이해가 필요한 부분인 것 같다.

이 논문 framework가 제안하는 것은 '서로 경쟁하는 모델'이다. discriminative model은 경찰과 같이 sample이 generative model에서 왔는지 real image에서 왔는지 결정하는 것을 배우고 generative model은 위조지폐범과 같이 discriminative model을 속이위해 노력한다.
- GAN하면 항상 나오는 경찰과 위조지폐범의 예시가 나오는 부분이다.


이 프레임워크에는 수많은 모델의 training algorithm과 optimization algorithm을 사용할 수 있다. 해당 논문에서는 random noise를 MLP에 통과시켜 sample을 생성하는 generative model과 똑같이 MLP로 구성된 discriminative model을 살펴본다.
- Ian Goodfellow는 이미 해당 프레임 워크가 다양하게 사용될 수 있다는 사실을 알고 있었다. 하지만 이렇게 까지 다양하게 연구 될 것을 알고 있었을지 궁금하다.
2. Related work
Related work부분에서는 이전까지 수행됐던 generative model에 관한 review가 진행된다. 나는 아직 배움이 부족하여 이 부분을 뛰어 넘도록 하겠다. 추 후에 related work에 등장하는 Boltzmann machine과 restricted Boltzmann machines, MCMC에 관해서는 ML/DL의 이해를 한층 더 업그레이드 시켜줄 개념이라고 생각해서 따로 다루려고 한다.(공부해야지..)
3. Adversarial nets

Data x에 대해 generator의 분포 $ P_g $를 배우기 위해 먼저 noise 변수 $ P_z(z) $를 정의한다. 그리고 $ z $를 $ G(z; \theta_g) $에 맵핑 시키는데 G는 미분 가능한 함수로 파라미터 $ \theta_g $를 갖는 MLP로 나타난다. MLP로 이루어진 $ D(x; \theta_d) $도 정의하는데 output은 scalar이다(위조 아니면 진짜). $ D(x) $는 x가 real image에서 나온 확률을 나타낸다. D를 real image와 G에서 나온 sample에 올바른 라벨을 붙일 수 있게 학습시키고 $ log(1 - D(G(z))) $를 minimize시키게 G를 훈련시킨다.
정리하자면
- noise 분포 $ P_z $ 에 $ z $ 를 입력으로 넣어 $ P_z(z) $ noise를 생성한다.
- noise를 G에 input으로 넣는다. G는 $ \theta_g $를 파라미터로 갖는 MLP이다.
- D는 real image와 G가 생성해낸 fake image를 구별할 확률을 최대화 한다.
- G는 $ log(1 - D(G(z))) $를 최소화 하도록 한다. --> $ D(G(z)) $는 D가 G에서나온 fake image를 구별하는 과정이다. 따라서 G의 입장에서는 자신이 만든 fake image가 D는 구별할 수 없도록 즉, real image label인 1을 scalar로 내뱉도록 만들어야 한다. 따라서 $ log(1 - 1) $은 $ - \infty $로 최소화되도록 G가 노력하는 것이다.
이 논문의 핵심이 되는 수식이 들어있는 부분이다. 먼저 용어에 대해 정리하자면
- $ P_{data} $는 real image의 확률분포이고 $ P_z $는 noise의 확률분포이다.
- $ E_{x \sim pdata(x)} $는 $ x $가 $ P_{data} $에서 왔다는 뜻으로 $ E_{x \sim Pdata(x)}[logD(x)] $는 D가 x를 Pdata 즉 real image에서 가지고 왔다고 판단할 확률의 기댓값이다.
- 비슷하게 $ E_{z \sim P_z(z)}[log(1 - D(G(z))] $는 D가 G(z)즉 noise를 통해 생성한 fake image를 fake image로 판단할 확률의 기댓값이다.
따라서 D는 기댓값을 maximize 즉, $ E_{x \sim Pdata(x)}[logD(x)] $에서는 D(x)를 1(real image)로 판단하고 $ E_{z \sim P_z(z)}[log(1 - D(G(z))] $에서는 D(G(z))를 0(fake image)로 판단하도록 하는 것이고, G는 기댓값을 minimize 즉, $ E_{z \sim P_z(z)}[log(1 - D(G(z))] $에서 D(G(z))를 D가 1(real image)로 판단하도록 노력해야한다는 것을 수식으로 나타냈다.
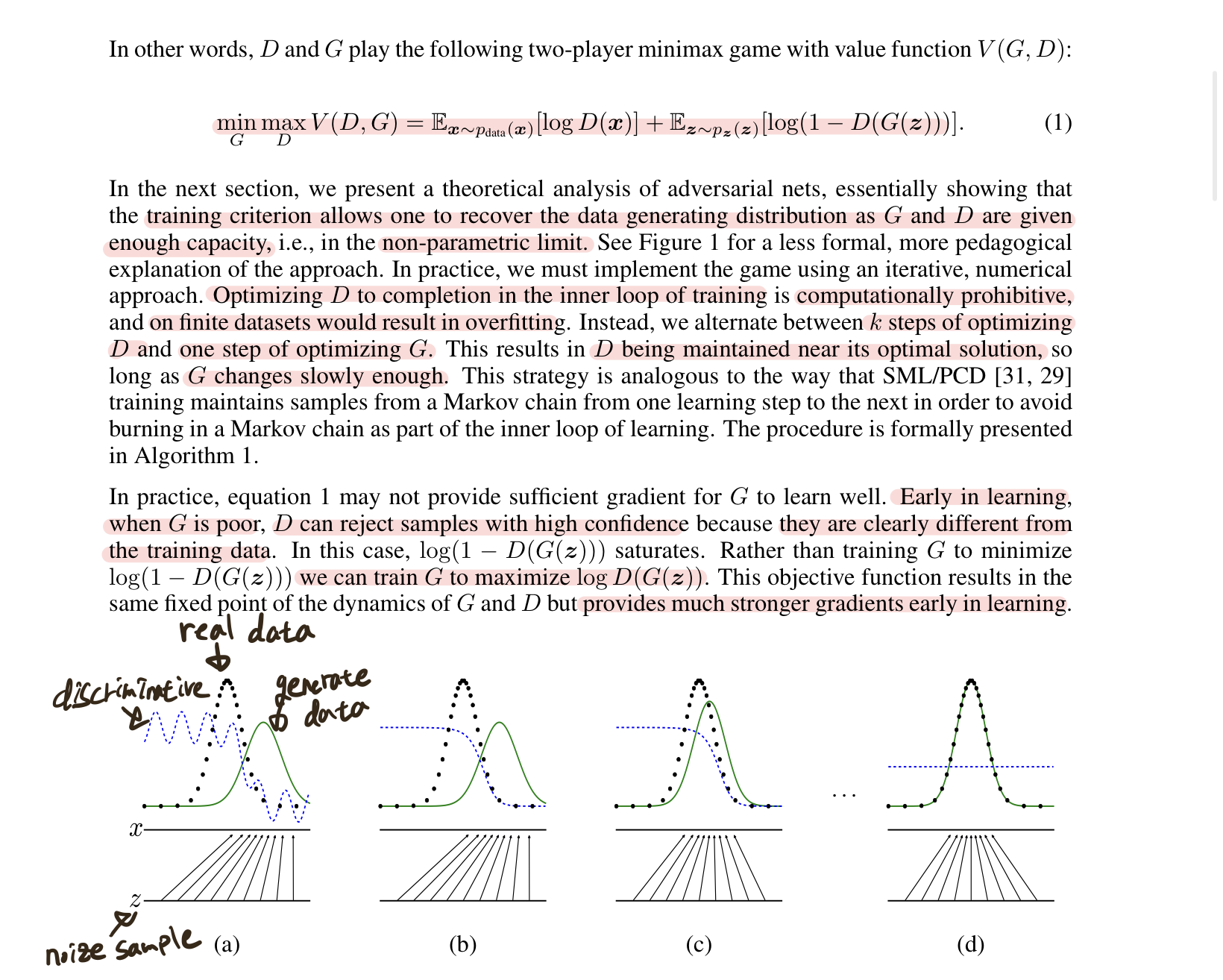
그림을 보면 직관적으로 이해하기 편한데 초기 step (a)에서는 noise z에대해 generator가 생성한 분포(green)가 real image 분포(black)와 다르기 때문에 discriminator가 잘 구분하지만 (d)로 갈수록 real image분포를 generator가 학습학 때문에 discriminator가 구분하지 못하는 것을 볼 수 있다.
논문에서는 하나의 문제점을 지적하는데 초기의 generator는 real image 분포와는 전혀 다른 분포를 갖는다는 점이다. 이로 인해 discriminator는 real과 fake를 구분하기가 너무 쉽고 학습이 제대로 진행되지 않는 상황이 발생한다. 이를 해결하기 위해 $ log(1-D(G(z)) $대신 $ log(D(G(z)) $를 사용하고 G는 이 기댓값을 최대화 하도록 만드는 것을 제안했다. 왜그런지 그림으로 보면

$ D(G(z)) = x $라고 한다면 초기에는 G(z)가 너무 형편없기 때문에 D(G(z))는 거의 0에 가까운 값을 내뱉을 것이다. 왼쪽그림을 보면 0에서의 미분값을 너무 작기때문에 학습을 할수록 D와 G의 학습이 차이날 것이다. 따라서 오른쪽과 같이 $ log(D(G(z)) $를 이용하면 G는 D(G(z))가 1이 되도록 즉, 기대값을 maximize하도록 바꿔주는 trick을 이용해야 하는 것이다.
추가로 논문에서는 training loop안에서 D가 완성되어 최적화 되는 것을 금지한다고 하는데 이는 D가 overfitting을 발생 시키기 때문이라고 한다. 따라서 D를 최적화하는 k단계와 G를 최적화 하는 단계로 훈련을 시켜야 한다고 주장한다.
- 의문. D가 overfitting되는 이유가 data의 수가 적기 때문인가? 그렇지 않고서야 D를 k번 훈련 더시키면 더 overfitting되는게 아닌가? 공부를 더 해봐야 할 것 같다.
4. Theoretical Results

Generator G는 fake image의 분포 $ P_g $를 암묵적으로 적의한다. 따라서 충분한 용량과 training시간이 주어지면 Algorithm1을 좋은 추정치로 수렴시킬 수 있다.
여기서 증명이 등장하는데 4.1에서 $ P_g = P_{data} $ 즉, fake image의 분포는 real image의 분포로 최적해를 갖는가?에 대한 증명과 4.2에서 Algorithm1이 최적해를 찾는가? 에대한 증명이 있다. 이는 다음 포스팅에 따로 다루도록 하겠다.(굉장히 어려운 부분이라고 생각된다..)

알고리즘을 보면 가장 먼저 epoch를 정하고 D를 training하기 위한 k step을 반복한다. k step마다 noise에서 m개를 가져오고 real image에서 m개를 가져와 'discriminator만' update한다. k step을 반복한 후에는 noise에서 m개를 가져와 'generator 만' update한다. 다음 글에서는 더 열심히 공부해서 위의 증명과 함께 알지 못했던 여러 숨겨진 지식들을 찾아보려고 한다.
https://89douner.tistory.com/329 이분께서 GAN을 정말 퀄리티 있게 다뤄주셨다. 다음포스팅에 열심히 공부해서 와야겠다..




