| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 선택정렬 증명
- Selection Sort
- ChatGPT 설명
- 이진탐색 증명
- Discrete Wavelet Transform
- chatGPT
- 선택정렬
- haar matrix
- binary search
- Proof Selection Sort
- 이진탐색
- Binary Search Proof
- BERT
- GPT-3
- Today
- Total
Just Do IT
[논문리뷰] Restricted Boltzmann Machine(RBM)와 Deep Belief Network(DBN) 본문
[논문리뷰] Restricted Boltzmann Machine(RBM)와 Deep Belief Network(DBN)
풀용 2023. 10. 8. 14:59들어가며
Deep Belief Network(이하 DBN)는 제한된 볼쯔만 머신이라고도 불리는 Restricted Boltzmann Machine(이하 RBM)을 여러 층 쌓아 학습시킨 모델로 2006년 Hinton 교수가 연구하여 논문이 나온 Generative model(생성모델)입니다.
현재는 RBM의 방식은 잘 사용하지 않지만 현재의 딥러닝 구조와 상당히 유사하고 RBM을 여러층 쌓은 Deep Belief Network은 AutoEncoder의 전신이라고 불릴 정도로 구조와 역할이 닮았습니다.
Neural Network가 지금처럼 활발히 연구가 되기전 weight의 초기화는 모델 학습에 있어서 엄청나게 중요한 요소였습니다. (물론 현재에도 마찬가지로 weight의 초기화는 굉장히 중요한 요소지만, Batch Normalization과 같은 기법이 등장하면서 초기값에 덜 민감하게 되었습니다) 이러한 상황에서 RBM을 여러층 쌓은 DBN으로 초기 가중치를 학습하고 이후에 neural network를 학습시켰을 때 기존 NN보다 빠르고 효과적으로 학습시킬 수 있었고 DBN이 초기 NN의 weight 초기화에 사용되었다고 합니다.
1. Generative Model
생성모델은 기본적으로 확률 분포를 학습한다고 볼 수 있습니다. 현재 많이 알려져있는 Variational AutoEncoder, GAN, Diffusion Model 모두 방법에는 차이가 있지만 특정 확률 분포를 학습하기 위한 모델입니다.

위의 그림처럼 차라고 하면 동그란 모양의 바퀴, 사이드미러, 문 등등 우리가 차라고 인식할 수 있게 할만한 요소들이 있습니다. 간단히 생각하면 바퀴는 동그라미일 '확률'이 굉장히 높기 때문에 바퀴를 동그랗게 그려줄 확률 분포가 나온다고 할 수 있습니다. 이렇게 차를 차답게 만들어 줄 수 있는 확률 밀도함수가 있다면 모델은 이 함수를 학습하는게 목표이고 이 함수에서 Sampling을 한다면 차가 정확하게 generate된다고 볼 수 있습니다.
2. Boltzmann Machine

Boltzmann Machine은 확률밀도함수의 학습을 위해서 입력노드인 Visible Node(위에서의 v)와 은닉층인 Hidden Node(위에서의 h)을 갖습니다. 만약 이미지가 binary 이미지이면 visible node는 0과 1을 갖을 수 있습니다. 하지만 위와 같은 모델은 계산하기가 너무 복잡하다는 문제가 있습니다. 이를 해결하기 위해 상대적으로 덜 엄격한 모델을 만들었습니다. 그 모델을 Restricted Boltzmann Machine이라고 합니다.
3. Restricted Boltzmann Machine
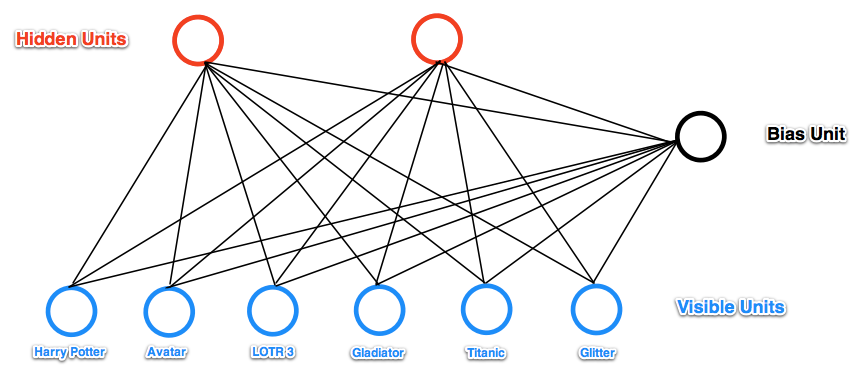
RBM은 Boltzmann Machine에서 visible unit끼리, hidden unit끼리의 연결을 없애 Bipartite형태로 만든 모델이라고 할 수 있습니다. 많은 RBM 논문에서와 강의안에서 RBM의 unit은 0 아니면 1을 갖는 binary 형태로 가정을 한다고 합니다. 본 포스팅에서도 binary unit을 가정하겠습니다.
3-1. RBM의 구성요소
RBM은 visible units, Hidden Units과 각각의 bias 벡터를 갖고, visible units과 hidden units를 연결하는 weight matrix를 갖습니다. 밑의 그림처럼 3개의 visible units와 2개의 hidden units를 갖는 모델이 있다면 visible units와 bias는 길이가 3인 vector를 갖고, hidden units와 bias는 길이가 2인 vector를 갖습니다. 그리고 이 둘을 연결하는 3x2의 weight matrix를 갖게 됩니다.

3-2. RBM의 Energy
모델을 학습시키기 위해서는 cost function이 존재해야 합니다. RBM은 Energy를 이용해서 cost function을 정의하게 되는데, 이는 물리학에서 차용한 개념이라고 합니다.(저는 문과 출신이라 잘 모르겠습니다...)
$$ E(v,h) = -b^tv-c^th-h^tWv $$
결국 우리는 input x에 대한 분포를 학습하기를 원하기 때문에 input x로 들어가는 visible unit의 확률을 높이는 방향으로 학습을 시켜야 합니다. 예를들어 28 * 28 MNIST 데이터 x가 있다고 하면, RBM에는 flatten된 784차원의 input이 visible unit으로 들어가게 될 것이고 우리는 이러한 input의 확률을 높이는 방향으로 학습을 시켜야 하는것입니다.
그러면 학습이 잘 되는지는 어떻게 알까요? 바로 이 때 energy가 이용됩니다. 볼츠만 energy는 낮을 수록 안정적인 상태를 유지하는데(물리적 개념) 똑같이 학습시키는 모델이 우리가 원하는 Input에 대해서 안정적인 상태를 유지시키기 위해 Energy가 낮아지는 쪽으로 학습을 시킵니다. 정리하자면 우리는 input 데이터에 대한 확률 $ P(v) $ 을 높이기 위하여 energy는 낮아지는 방향으로 학습을 시키는 것입니다.

위의 그림의 예를 들어 Energy를 계산해 보면 -0.7이라는 값이 나옵니다. 근데 -0.7은 안정적인 상태일까요? 우리는 이를 확률로 표현하고 싶어집니다. 이를 수식으로 써보면

- 결국 input 확률 p(v)를 구하고 싶다.
- 이를 joint로 나타내면 $ p(v,h) $ 에 대하여 모든 h를 합친 것으로 표현할 수 있다.
- 그걸 다시 energy로 표현하면 가장 오른쪽 식이 되고 먼저 주황색 부분부터 살펴 보겠다.
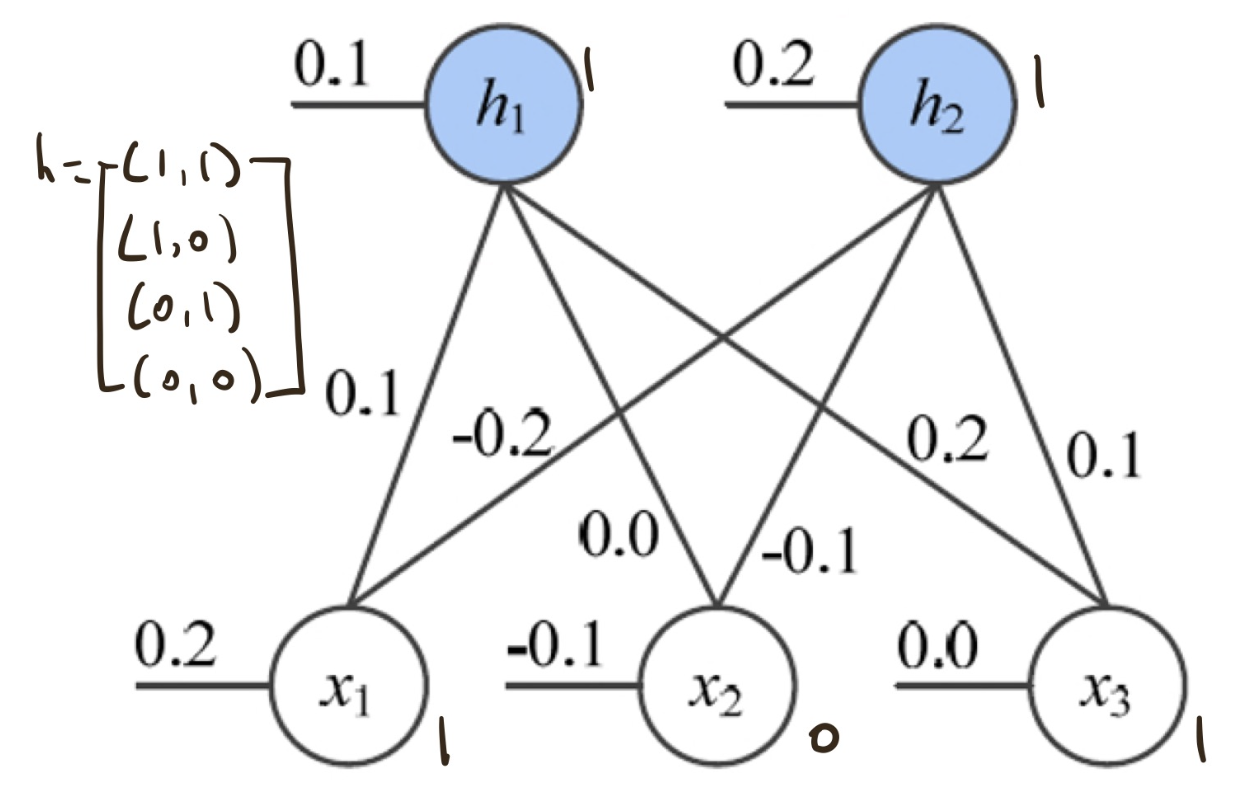
먼저 energy는 낮아질 때 확률은 높아져야 함으로 Energy함수에 -를 붙여주고, softmax 함수 처럼 확률로 나타내기 위해 exponential과 Z를 도입합니다. 전체적으로 softmax와 비슷한 느낌으로 보면 좋을 것 같습니다.
주황색 부분은 어떤 한 visible input에서 나올 수 있는 모든 hidden의 경우의 수를 구하고 Energy를 합한 값입니다.
예를들어 위 그림처럼 visible이 [1,0,1]이 들어왔을 때 모든 hidden의 경우의수 (0,0) ~ (1,1)의 energy를 다 구해서 더하면 p(v) 하나를 알 수 있게 됩니다.
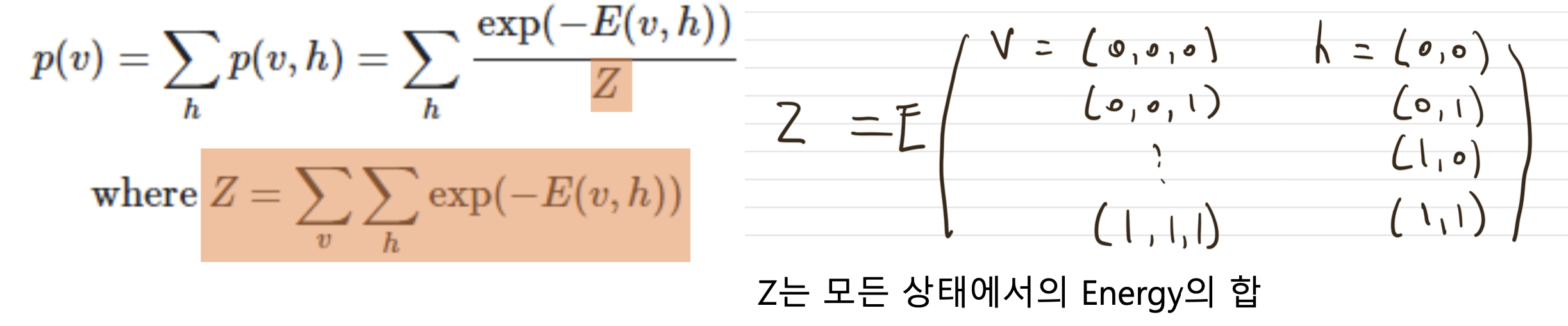
그리고 분모 Z의 부분은 모든 visible과 hidden의 경우의수를 다 구해서 모든 Energy를 합한 값입니다. 결국 softmax와 비슷하게 해당 (visible의 energy / 모든 경우의 energy)를 계산함으로써 확률로 표현할 수 있게 되는것입니다.
3-3. 수식 전개

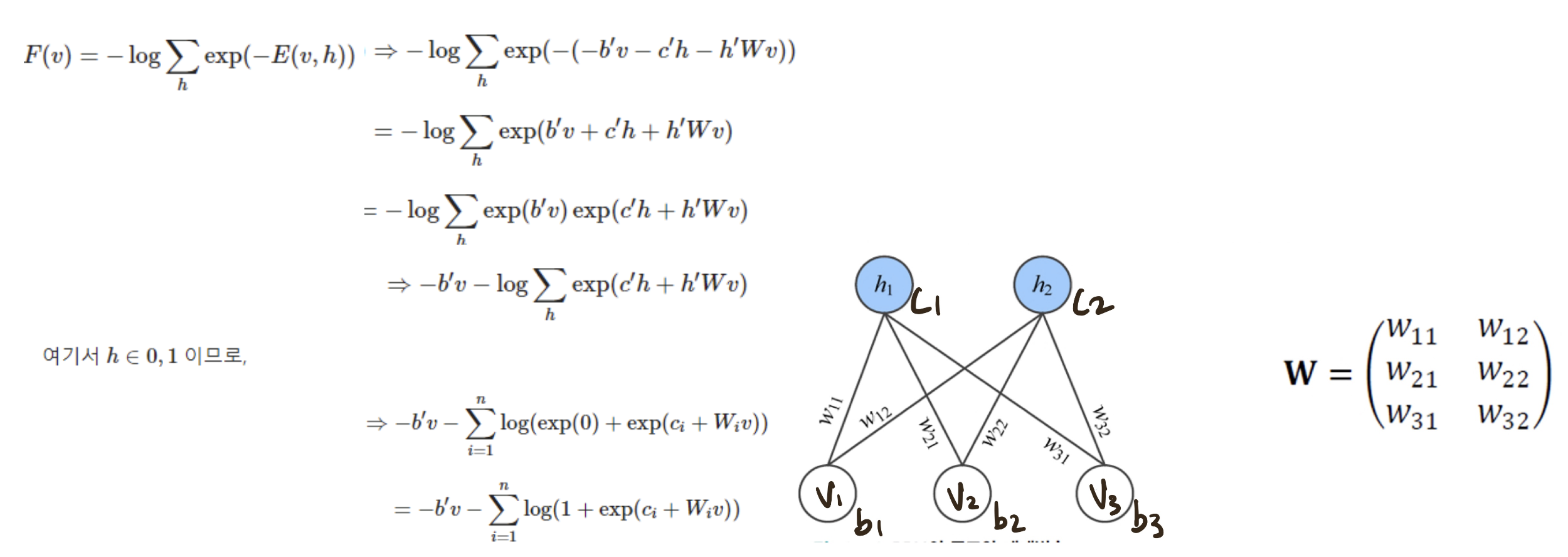
우리가 앞에서 구했던 P(v)를 오른쪽과 같이 바꿔 쓸 수 있습니다. 이는 나중에 계산 편의성을 위해 바꾸는 과정입니다. 결국 핵심은 -E(v,h)를 F(v)의 형태로 바꾸는 식입니다. 이를 Free energy라고 합니다.
4.1 Sampling 방법
이제 어떻게 visible에서 hidden으로의 sampling을 진행하고, hidden에서 visible로 sampling을 진행할지에 대해서 알아보겠습니다. 흔히 현재 사용하는 Feed Forward Network처럼 wx * b를 진행하고 activation을 씌우면 되지 않나? 라고 생각 할 수 있지만, 엄연히 RBM은 현재의 FFN과는 다른 매커니즘으로 만들어졌기 때문에(Energy, 양방향 연결) Sampling 방법을 수식으로 유도해야합니다.
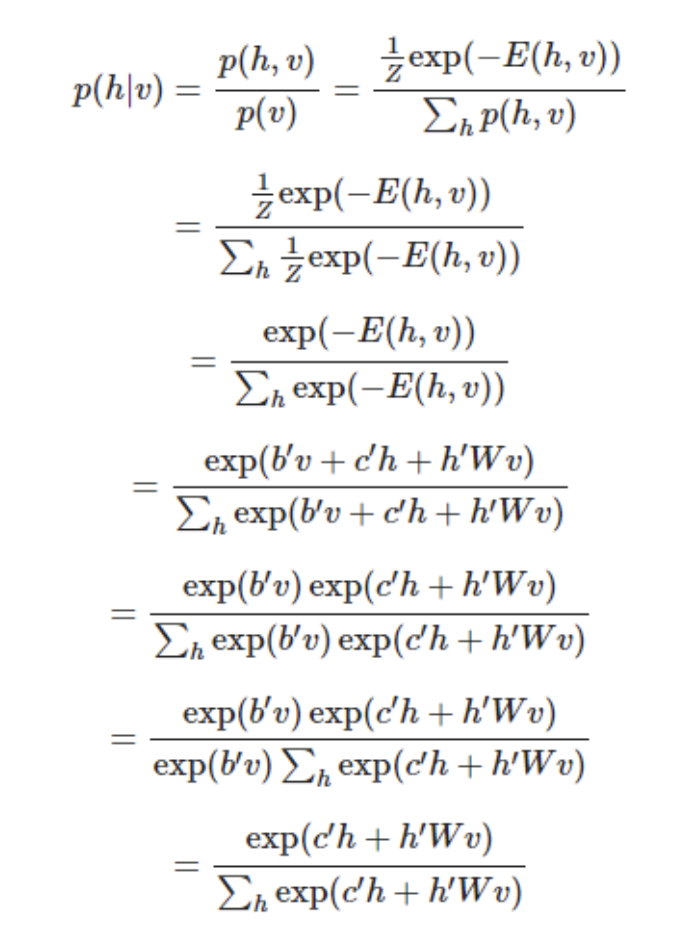
조건부 확률 v가 들어왔을 때의 h를 Energyg함수를 사용해 쭉 풀면 위와 같이 됩니다. 이때 총 n개의 hidden unit중에 i 번째 unit이 1이될 확률을 계산하면

분모 h는 0과 1의 값을 갖으므로 풀어서 써주고 식을 전개하면 신기하게도 W*x + b에 sigmoid를 씌운 형태가 나오게 됩니다. 마찬가지로 h에서 v로의 sampling 또한 같은 형태를 띄게 됩니다.
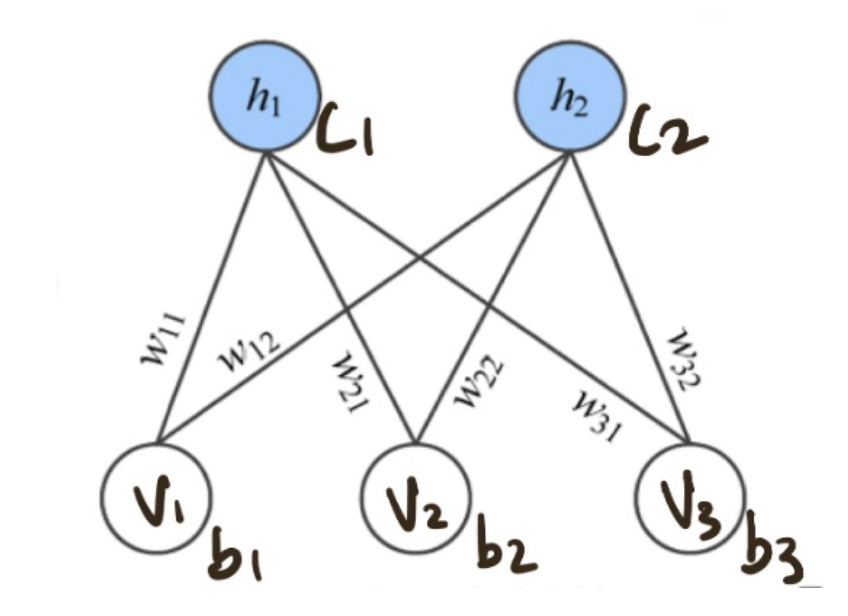
위 그림으로 예를 들면 1번째 hidden unit h1이 1이될 확률은 P(h1 = 1 |v) = sigmoid(W1*v + c1) 이 되는 것입니다.
여기서 주의해야할 점은 Sigmoid function output이 현재 DNN에서는 Deterministic하게 0.5가 넘으면 1로, 아니면 0으로 판별하지만 여기서는 '확률'로 표시됩니다. 예를 들어 output이 0.7이 나왔으면 해당 node는 0.7의 확률로 1의 값을 갖고 0.3의 확률로 0의 값을 갖습니다.
5. 학습 과정
그렇다면 학습의 loss는 어떻게 정해야 할까요? 바로 Maximum likelihood를 사용합니다.
Maximum Likelihood Estimation(MLE) 이해해보기
공돌이의 수학정리노트 님의 포스팅을 보고 나름대로 정리한 글 입니다. MLE란? MLE는 Maximum Likelihood estimation이라고 하고 한국말로는 최대 우도 추정 혹은 최대 가능도 추정이라고 한다.(개인적으
rla020.tistory.com
만약 파라미터가 잘 학습됐다면, 현재 데이터를 가지고 얻은 likelihood가 최대일 것입니다. 이를 위해서 likelihood를 미분하여 파라미터를 찾는 과정은 위의 포스팅에 올려져 있습니다. 이를 적용하면,
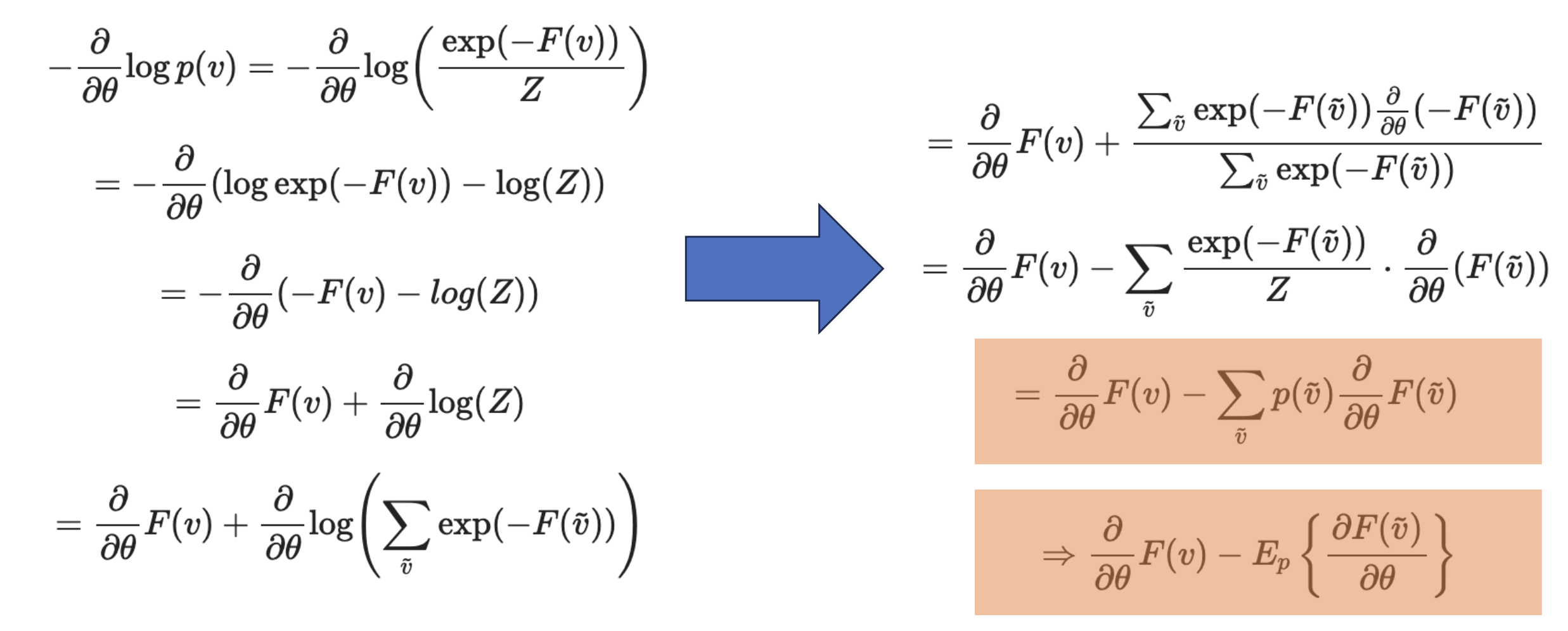
위와 같이 수식을 전개할 수 있고, 결국 visible unit의 free energy에서 reconstruct된 visible unit의 기댓값을 빼는 방식이 됩니다.

기댓값은 구하기 힘들기 때문에 여러번 smapling해서 mean을 취하면 근사시킬 수 있습니다.
정리하자면, likelihood를 maximize시키는 것은 visible unit의 free energy에서 reconstruct visible unit의 기댓값을 빼면 되고, 이론상 reconstruct visible unit을 무한히 많이 반복해야 제대로된 기댓값을 구할 수 있는 것입니다. 하지만 Hinton 교수님은 실험적으로 1번의 sampling 만으로도 좋은 효과를 내는 것을 알아냈고, 최종적으로 Loss는
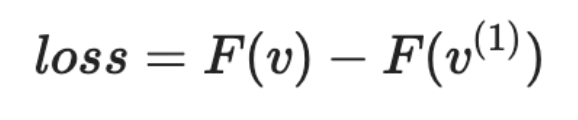
밑의 식을 사용하게 됩니다.
6. 최종 정리

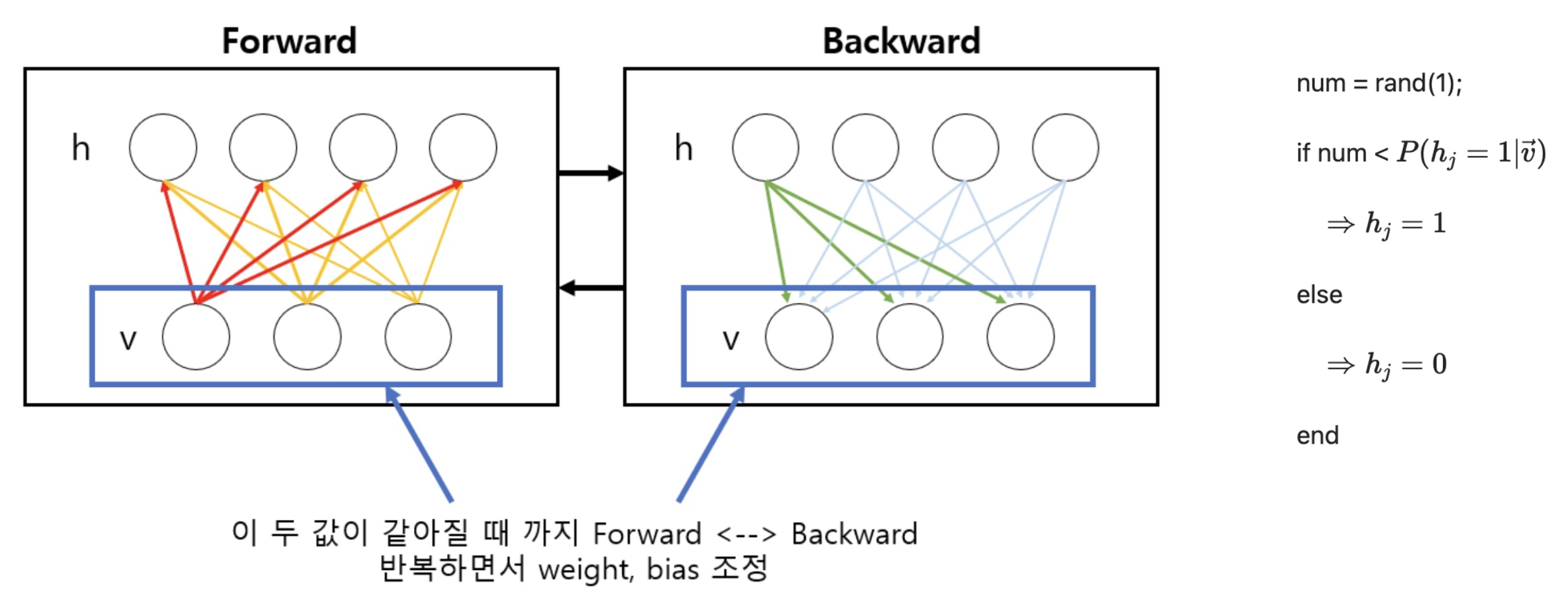
- v에서 h로 sigmoid(W*v + c)
- h에서 v로 sigmoid(W*h + b)
- v의 free energy - reconstruc v의 free energy
- backpropagation
- 이 때 각 unit은 deterministic한 값이 아니라 stochastic하게 0과 1의 값을 갖는다.
7. Deep Belief Network
위의 RBM을 여러층 쌓은 모델을 DBN이라고 합니다. 초기 weight initialization 기술이 없던 시절 gradient vanishing을 어느 정도 해결하는 weight initialization 방법으로 DBN을 사용했다고 합니다. DBN은 두가지 단계를 갖습니다.
첫번째 단계는 pre-train 과정으로 RBM을 한층씩 쌓아갑니다.

먼저 x - h1 - x로의 input x를 reconstruct하고, 학습이 완료되면 x - h 사이의 weight 는 freeze시켜놓고 h1 - h2 - h1 로의 h1을 reconstruct 하고를 쭉 반복하여 weight 를 초기화 합니다. 이후 목적에 맞게 Fine-tuning하여 사용하게 됩니다. 기본적인 classification 문제는 오차 역전파를 통해 Fine-tuning이 됩니다. 현재의 transfer learning 방식과 어느정도 유사하다고 보면 좋을 것 같습니다.(wieght가 적절하게 초기화 되있는 상태에서 내 task에 맞게 fine-tuning하는 방식)




